Research Summaries
Context and Motivation for Smart Grid Controls
Electric power systems have traditionally been designed as vertical hierarchies, where power flows unidirectionally through the grid from bulk generation to consumers, and high-inertia synchronous generators provide and reinforce system stability. Presently however, environmental concerns and technological advance are disrupting these traditional architectures, with small-scale distributed generation (DG) supplanting synchronous generators and causing bidirectional power flow. Production from DG is variable, intermittent, and difficult to predict over long time scales. The fundamental modern control challenge is then to reliably balance supply and demand over both short and long time scales, while satisfying physical and economic constraints. Due to the high capital costs of infrastructure upgrades, a software-powered smart grid is the most cost effective direction for meeting these challenges.
Our research attacks these sustainability problems from a first principles point of view, and considers both analysis and design. The overarching goal is translate modern advances in automatic control and optimization into simple, intuitive, and reliable methodologies for power system control. Below are some sample projects.
Distributed Control in Microgrids and Power Systems
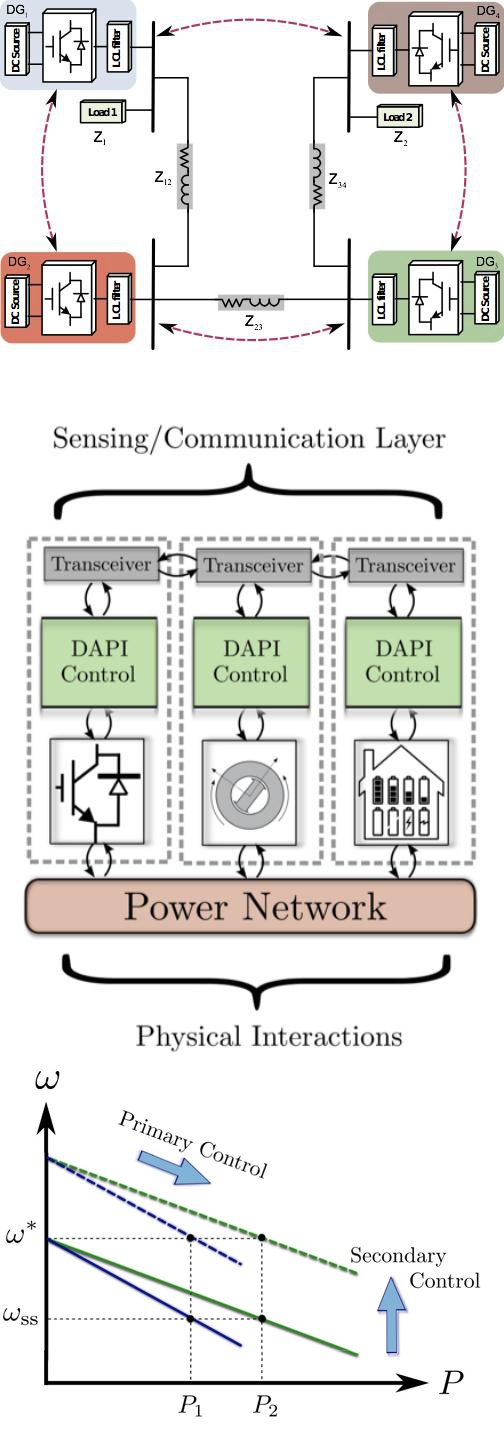 |
Electric power grids are transitioning from an era of bulk, centralized power generation to one dominated by small-scale distributed generation (DG). While classic high-inertia rotating machines provided a reliable backbone for the grid, resisting the disturbances caused by variable consumption, DGs integrated through power electronics are inherently volatile. Barring costly distribution system upgrades, current best control practices in which DGs ignore the stability of the common grid infrastructure will be insufficient to accommodate the rise of rooftop solar, leading to frequent system failures. If a safe transition to open-access distribution systems is to be made, these conventional approaches to DG integration must be rethought and modernized to become more grid-conscious, while respecting legacy functionality. A key problem is to maintain a reliable grid in an open-market environment interfacing tens of thousands of volatile DGs. Moreover, with the rise of cheap power electronics, thousands of possible measurement and control points are now available, and central grid management will need to make room for scalable distributed control solutions. Our work in this area has focused on controller designs which allow DG to enhance system stability, rather than compromise it. At level of primary droop control we have developed the first analytical techniques to assess the existence and stability of system equilibria, and connected these decentralized droop controllers to optimization algorithms for economic dispatch. At the secondary control level, we have developed coordination algorithms in which DG units communicate to collectively perform optimal frequency regulation and voltage support while balancing active and reactive power demands across units. The designs require no fine-tuning, come with performance guarantees, and have been extensively validated in experimental test-beds. With the requirement of a centralized controller eliminated, these distributed controllers may scale to thousands of interconnected devices while maintaining system stability. These designs may help reduce the lengthy interconnection approval times for DG, allowing renewable penetration to scale without worries of instability and without significant overhead costs for grid operators. Here are some representative slides, and another blurb on this project. Some of our publications on this topic are J. S. Gomez, D. Saez, J. W. Simpson-Porco, and R. Cardenas. Distributed Predictive Control for Frequency and Voltage Regulation in Microgrids. IEEE Transactions on Smart Grid. Note: To appear. [Manuscript] [BiBTeX] M. Farrokhabadi, J. W. Simpson-Porco, and C. A. Canizares. Optimal Design of Voltage-Frequency Controllers for Microgrids. IEEE Transactions on Smart Grid. Note: Submitted. [Manuscript] [BiBTeX] J. W. Simpson-Porco, Q. Shafiee, F. Dörfler, J. C. Vasquez, J. M. Guerrero, and F. Bullo. Secondary Frequency and Voltage Control in Islanded Microgrids via Distributed Averaging. IEEE Transactions on Industrial Electronics, 62(11):7025-7038, 2015. [Manuscript] [BiBTeX] F. Dörfler, J. W. Simpson-Porco, and F. Bullo. Breaking the Hierarchy: Distributed Control & Economic Optimality in Microgrids. IEEE Transactions on Control of Network Systems, 3(3) 241-253, 2016. [Manuscript] [BiBTeX] M. Todescato, J. W. Simpson-Porco, F. Dörfler, R. Carli, and F. Bullo. Voltage Stress Minimization by Optimal Reactive Power Control. IEEE Transactions on Control of Network Systems, 5(3):1467-1478, 2018. [Manuscript] [BiBTeX] J. W. Simpson-Porco, F. Dörfler, and F. Bullo. Synchronization and Power Sharing for Droop-Controlled Inverters in Islanded Microgrids. Automatica, 49(9):2603-2611, 2013. [Manuscript] [BiBTeX] J. W. Simpson-Porco, F. Dörfler, and F. Bullo. Voltage Stabilization in Microgrids via Quadratic Droop Control. IEEE Transactions on Automatic Control, 62(3):1239-1253, 2017. [Manuscript] [BiBTeX] J. W. Simpson-Porco and F. Bullo. Distributed Monitoring of Voltage Collapse Sensitivity Indices. IEEE Transactions on Smart Grid: Special Issue on Theory of Complex Networks with Application to Smart Grid Operations, 7(4):1979–1988, 2016. [Manuscript] [BiBTeX] |
Solvability of Power Flow Equations
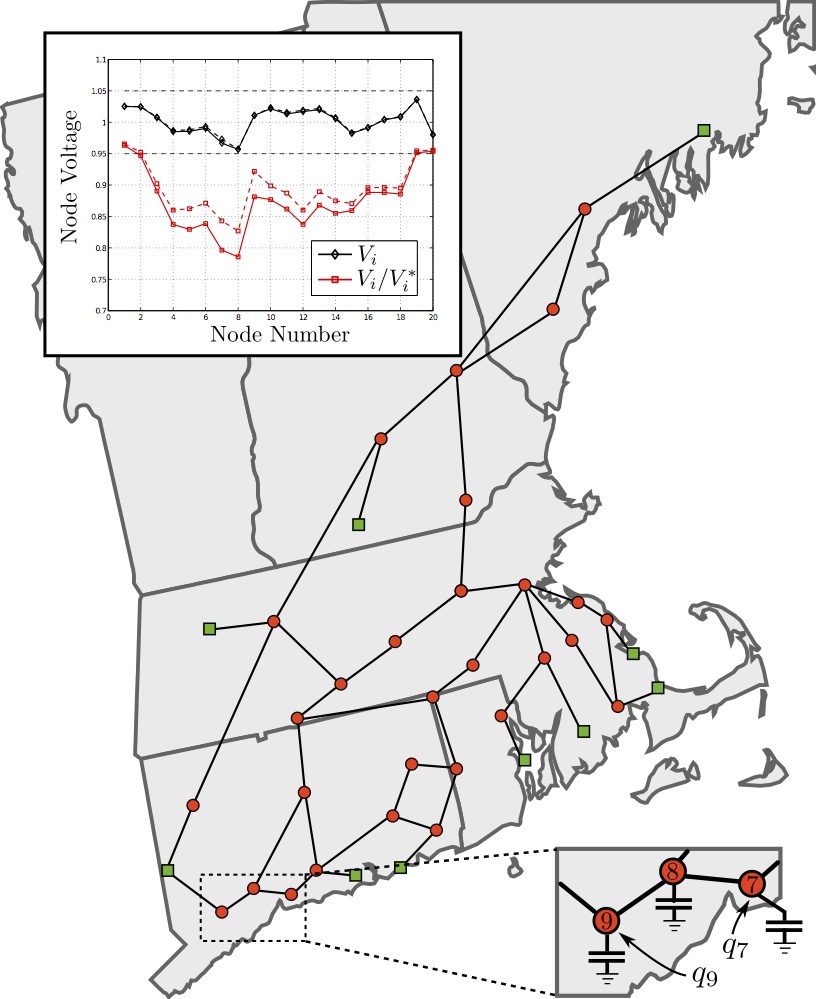 |
The solution spaces of power flow equations are complex and multi-valued. While the practical operating point of the network is typically at high-voltage with small phase differences along transmission lines, the distance between this desirable operating point and unstable low-voltage operating points quickly shrinks under increased loading, degrading stability margins. Quantifying this stability margin in both parameter and voltage-space is a key requirement for both planning and monitoring of transmission networks. While accurate numerical techniques exist to asses this stability margin, they offer little theoretical insight into how the structure of the grid influences (in)solvability. Our current work in this area focuses on developing precise and physically intuitive algebraic conditions under which the power flow equations possess a unique, high-voltage solution, along with a guaranteed robustness margin against bifurcation. These conditions lead immediately to voltage collapse proximity indicators and loading margins, lower-bounding the distance to the insolvability boundary in both state-space and parameter-space. The key insight is to carefully take into account the relative locations of generation and load by encoding the grid topology, impedances, generator voltage set points into a ‘stiffness’ matrix. The interplay between this stiffness matrix and the scheduled power demands provides the required multi-bus generalization of the loadability limit from the one-load-one-generator model. Some of our publications on this topic are J. W. Simpson-Porco. A Theory of Solvability for Lossless Power Flow Equations – Part I: Fixed-Point Power Flow. IEEE Transactions on Control of Network Systems, 5(3):1373-1385, 2018. [Manuscript] [BiBTeX] J. W. Simpson-Porco. A Theory of Solvability for Lossless Power Flow Equations – Part II: Conditions for Radial Networks. IEEE Transactions on Control of Network Systems, 5(3):1361-1372, 2018. [Manuscript] [BiBTeX] J. W. Simpson-Porco. Lossy DC Power Flow. IEEE Transactions on Power Systems, 33(3):2477-2485, 2017. [Manuscript] [BiBTeX] K. Dvijotham, E. Mallada, and J. W. Simpson-Porco. High-voltage solution in radial power networks: Existence, properties and equivalent algorithms. IEEE Control Systems Letters, 1(2) 322–327, 2017. [Manuscript] [BiBTeX] J. W. Simpson-Porco, F. Dörfler, and F. Bullo. Voltage Collapse in Complex Power Grids. Nature Communications, 7(10790), 2016. [Manuscript] [BiBTeX] |
Systems and Control Theory
I am interested in fundamental research in systems and control theory, including nonlinear control theory, distributed control systems, and optimization-based control. The theory we develop is broadly motivated by problems arising in energy systems. Some of our publications on these topics are
J. W. Simpson-Porco. Equilibrium-Independent Dissipativity with Quadratic Supply Rates. IEEE Transactions on Automatic Control, 64(4) pages 1440-1455, 2018. [Manuscript] [BiBTeX]
F. Dörfler, J. W. Simpson-Porco, and F. Bullo. Electrical Networks and Algebraic Graph Theory: Models, Properties, and Applications. Proceedings of the IEEE, 106(5) 977-1005. [Manuscript] [BiBTeX]
L. S. P. Lawrence, J. W. Simpson-Porco, and E. Mallada. Linear-Convex Optimal Steady-State Control. IEEE Transactions on Automatic Control. Note: Submitted. [Manuscript] [BiBTeX]
J. W. Simpson-Porco, B. K. Poolla, N. Monshizadeh, and F. Dörfler. Input-Output Performance of Linear-Quadratic Saddle-Point Algorithms with Application to Distributed Resource Allocation Problems. IEEE Transactions on Automatic Control. Note: To appear. [Manuscript] [BiBTeX]
J. W. Simpson-Porco. Input/Output Analysis of Primal-Dual Gradient Algorithms. In Allerton Conference on Communication, Control, and Computing, Monticello, IL, pages 219-224, September 2016. [Manuscript] [BiBTeX]
J. W. Simpson-Porco and F. Bullo. Contraction Theory on Riemannian Manifolds. Systems & Control Letters, 65:74-80, 2014. [Manuscript] [BiBTeX]